js求最佳基因配对率

发表于 |

给出一个长度为10的由基因“ATGC”随机组成的参照字符串，然后再给出一个长度为6的可操作基因字符串，可操作字符串的字符顺序不能变，但是可以移动其位置，求移动字符串和参照字符串的最大配对率

题目来源

项目中的一个”基因“配对小游戏，如下：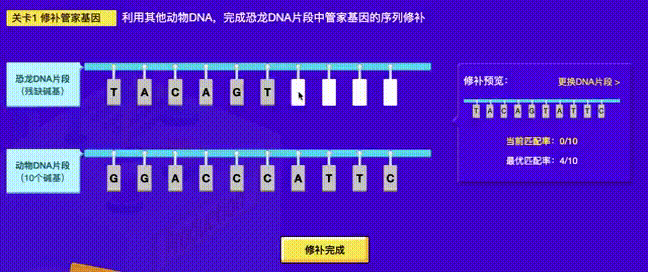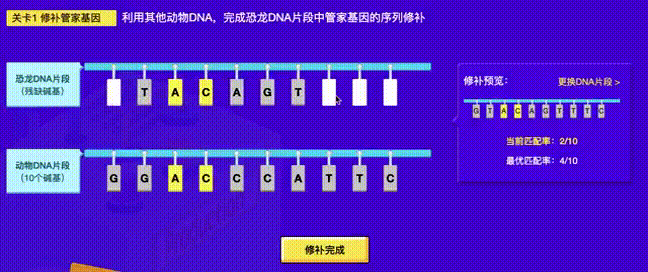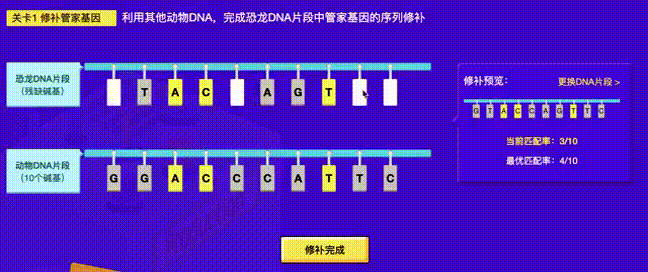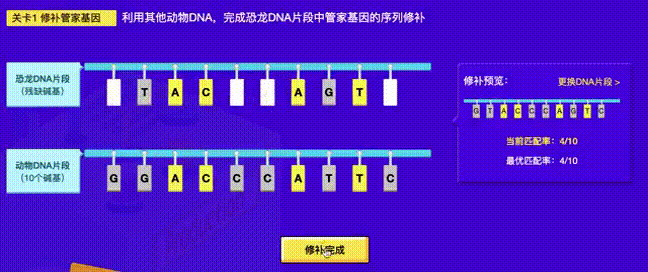

按上图中给出的例子：

  • 参考碱基序列为：GGACCCATTC
  • 可顺序移动碱基序列为：TACAGT****
  • 其中*可移动，匹配率 = 符合配对规则的字母个数 / 总字母个数
  • 当可移动碱基的位置为*TAC**AGT*时有和参考序列有4个碱基匹配，此时匹配率为：4/10，是最优匹配率

全组合

为了节省时间，项目中采取了全组合的方法，把所有情况列举出来，然后对比，取匹配率最高的一种情况作为答案。 转换一下就知道，题目等于是有10个位置，任意取四个放空白碱基，一共有C(10,4) = 10!/(4! * 6!) = 10 * 9 * 8 * 7 / (1 * 2 * 3 * 4) = 210种情况，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
function toCalculateBestPairingRatio() {
    const contrastGene = 'GGACCCATTC'.split('');
    const gene = 'TACAGT'.split('');
    let tempGene, curNum = 0;
    let bestPairingRate = {
        rate: 0,
        arrangement: ''
    };
    for (let i = 0; i < 10; i++) {
        for (let j = i + 1; j < 10; j++) {
            for (let k = j + 1; k < 10; k++) {
                for (let l = k + 1; l < 10; l++) {
                    tempGene = [...gene];
                    tempGene.splice(i, 0, '');
                    tempGene.splice(j, 0, '');
                    tempGene.splice(k, 0, '');
                    tempGene.splice(l, 0, '');
                    curNum = contrastGene.reduce((acc, cur, index) => acc + (cur === tempGene[index]), 0);
                    if (curNum >= bestPairingRate.rate) {
                        bestPairingRate.rate = curNum;
                        bestPairingRate.arrangement = tempGene;
                    }
                }
            }
        }
    }
    return bestPairingRate;
}

动态规划

全组合虽然能够解决本次问题，但是其复杂度为Ο(n!)，当基数再大一点的时候就不适合了。像这种求解最优的问题非常适合使用动态规划，把上题中的基因通过表格列出，行表示参考碱基序列，列表示可顺序移动碱基序列，从第一个碱基开始逐渐增加，表格内为最佳碱基配对率

j\iGGACCCATTC
T0000000111
A-011111111
C--02222222
A---0223333
G----022333
T-----02344

Row表示行，i为其下标，Col表示列，j为其下标，Rate表示最佳匹配率，通过观察可以发现规律：

Rate[j][i] = Max{Rate[j-1][i-1] + Number(Row[i] == Col[j]), Rate[j][i - 1]}
其中当只有一行时Rate[j-1][i-1] = 0，表格左下角则为最大的匹配率

1
2
3
4
5
6
7
8
9
10
11
12
function toCalculateBestPairingRatio() {
    const contrastGene = 'GGACCCATTC'.split('');
    const gene = 'TACAGT'.split('');
    let arr = []
    for (let j = 0; j < gene.length; j++) {
        arr[j] = []
        for (let i = j; i < contrastGene.length; i++ ) {
            arr[j][i] = Math.max((j == 0 ? 0 : arr[j-1][i-1]) + Number(contrastGene[i] == gene[j]), arr[j][i - 1] || 0)
        }
    }
    return arr[gene.length - 1][contrastGene.length - 1]
}

该方法的算法复杂度为平方阶，能够完美解决当前问题，就算后面的基数扩增也不怕了